Las Cajitas LIRO, unas cajitas que nos solucionan muchos problemas
Uno de los desafíos más grandes que tenemos los docentes cuando enfrentamos a los niños ante un problema matemático, es lograr que los niños comprendan el enunciado e identifiquen lo que éste le pide averiguar. El matemático húngaro George Polya es uno de los estudiosos que más aportó a la teoría de resolución de problemas. Polya generalizó su método en los siguientes cuatro fases o pasos: entender el problema, configurar un plan, ejecutar el plan y probar el resultado. En los últimos años, se ha ido difundiendo mucho esta ruta.
Conocemos la importancia de que los niños comprendan el problema. Solo su debida comprensión garantiza que pueda resolverlo con éxito, por ello, siempre estuvimos tratando de hallar formas y caminos para que los niños superaran esta primera fase, ya que la comprensión es la base de la resolución; si el niño no comprende el problema, no podrá llegar a una adecuada solución así se cuente con los mejores materiales, condiciones o métodos. Durante la resolución de cualquier problema, debe enfatizarse este proceso de comprensión (así nos tome más tiempo). Si logramos que los niños comprendan bien el problema, los siguientes procesos fluirán de manera ágil. Con base en esa convicción y en el afán de facilitar la comprensión de los problemas, varias veces propusimos a los niños dibujar lo que ellos habían entendido del problema. Esta estrategia era del agrado de los niños -recordemos que trabajamos con niños que se encuentran en proceso de transición del estadio pre-operatorio al de operaciones concretas-, a ellos les gusta expresarse mediante el dibujo y además su pensamiento es prevalentemente concreto, es decir, aprenden a través de experiencias manipulativas, las mismas que les permiten fijar aprendizajes.
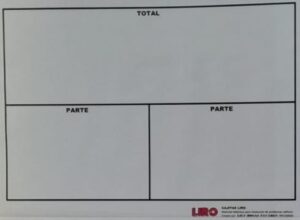 Fue así que trabajando en el aula de 2do grado una sesión de problemas de combinación e intentando que los niños comprendan el problema, notamos que su comprensión se facilitaba cuando mediábamos los procesos con dibujos que derivaron en un esquema que, con una lógica visual muy comprensible para los pequeños, representaran la relación entre los datos (en este caso, la relación de clase y subclase).
Fue así que trabajando en el aula de 2do grado una sesión de problemas de combinación e intentando que los niños comprendan el problema, notamos que su comprensión se facilitaba cuando mediábamos los procesos con dibujos que derivaron en un esquema que, con una lógica visual muy comprensible para los pequeños, representaran la relación entre los datos (en este caso, la relación de clase y subclase).
Viendo cómo esta representación gráfica del problema (ya teníamos el esquema de la combinación) ayudaba a la comprensión del problema, quisimos probar si estos esquemas ayudarían también en el momento de emplear estrategias para la resolución. Considerando que los niños aprenden manipulando objetos, nos animamos a trasladar el esquema de combinaciones al formato tridimensional usando una cajita de cartón. La pusimos a disposición de los pequeños para observar cómo la usaban en el momento de resolver un problema de combinación trabajando con sus fichas y tapitas. El resultado fue impactante y muy alentador, varios niños usaron la cajita y resolvieron correcta y rápidamente el problema.
Este tránsito del formato bidimensional al formato tridimensional, de la propuesta gráfica a la concreta fue pertinente ya que se ajustaba y respondía a las características de los estudiantes, cuyo pensamiento es concreto. Así fue como se creó la cajita de combinación, que representaba la relación parte-todo y que surgió del esquema que se había trabajado en la fase de comprensión. Los niños identificaron inmediatamente la estructura tridimensional (cajita en físico) asociándola al dibujo que les había ayudado a comprender el problema. Luego, nos animamos a elaborar cajitas para todos los niños del aula con ayuda de algunos papitos empleando cajitas de cartón forradas con papel de regalo. En la cajita movilizaban tapitas, material base 10 o regletas para representar los datos y los trasladaban por los compartimentos hallando rápidamente la solución. Esta experiencia en el aula nos permitió descubrir la facilidad con la que los niños comprendían y resolvían este tipo de problemas utilizando esta estructura o modelo matemático acompañado de material no estructurado (tapitas) o estructurado (base 10, regletas). Los niños nos estaban demostrando cuánto les ayudaba iniciar “dibujando el problema” para comprenderlo, y luego, emplear la estructura en físico para trabajar estrategias sobre ella usando material concreto ya sea estructurado o no estructurado. Esta experiencia nos animó a diseñar la estructura de los otros tipos de problemas aditivos (comparación, igualación y cambio) en formato tridimensional, puesto que ya ensayábamos “dibujos” de estos tipos de problemas.
 La segunda cajita que se construyó fue la cajita para problemas de comparación e igualación (que comparten la misma estructura). Para la comprensión del problema, ya estábamos trabajando en base a gráficos de barras y barras comparadoras. (ver anexo). No resultó sencillo trasladar la estructura gráfica hacia una representación concreta ya que se trataba de un proceso dinámico, por eso, esta cajita pasó por algunas variaciones hasta llegar a su diseño final. Estas modificaciones se dieron en función a la validación que se hacía directamente en el trabajo con los mismos niños en las aulas durante la resolución de este tipo de problemas. La ultima inclusión en este diseño (y que es un elemento que la hizo mucho más funcional), es la barrita removible separadora de los criterios de igualdad y diferencia que se evidencian durante la resolución de un problema de comparación o igualación. Esta barrita, al hacer muy visible la diferencia entre dos cantidades desiguales, hacía que los niños identificaran inmediatamente la solución del problema en el plano concreto. El reto estaba ahora en lograr el tránsito por los otros niveles de representación a partir de lo manipulado en la cajita. Se usaron los formatos bidimensionales para apoyar la representación gráfica de estos problemas. Finalmente, lo graficado, que proviene directamente de lo trabajado en concreto, se traduce a expresiones simbólicas (en consonancia con lo que propone la primera capacidad de la competencia de cantidad en el CNEB). La cajita complementaria “Falta” se usa para las situaciones de igualación.
La segunda cajita que se construyó fue la cajita para problemas de comparación e igualación (que comparten la misma estructura). Para la comprensión del problema, ya estábamos trabajando en base a gráficos de barras y barras comparadoras. (ver anexo). No resultó sencillo trasladar la estructura gráfica hacia una representación concreta ya que se trataba de un proceso dinámico, por eso, esta cajita pasó por algunas variaciones hasta llegar a su diseño final. Estas modificaciones se dieron en función a la validación que se hacía directamente en el trabajo con los mismos niños en las aulas durante la resolución de este tipo de problemas. La ultima inclusión en este diseño (y que es un elemento que la hizo mucho más funcional), es la barrita removible separadora de los criterios de igualdad y diferencia que se evidencian durante la resolución de un problema de comparación o igualación. Esta barrita, al hacer muy visible la diferencia entre dos cantidades desiguales, hacía que los niños identificaran inmediatamente la solución del problema en el plano concreto. El reto estaba ahora en lograr el tránsito por los otros niveles de representación a partir de lo manipulado en la cajita. Se usaron los formatos bidimensionales para apoyar la representación gráfica de estos problemas. Finalmente, lo graficado, que proviene directamente de lo trabajado en concreto, se traduce a expresiones simbólicas (en consonancia con lo que propone la primera capacidad de la competencia de cantidad en el CNEB). La cajita complementaria “Falta” se usa para las situaciones de igualación.
Por último, y después de probar la gráfica de las situaciones de transformación o cambio de varias maneras, quedó definida la estructura original y el diseño pa ra los problemas de cambio (a decir verdad, fue el que más nos hizo cavilar). Los resultados del trabajo con el esquema y la respectiva cajita han sido muy satisfactorios, han facilitado a los niños la comprensión y la resolución de los problemas de transformación en sus seis tipos. Lo más interesante es que ellos mismos pueden ejecutar nuevas y diversas formas de resolución para un mismo problema utilizando este material didáctico concreto. Reconocemos que la Cajita para problemas de cambio es la que más acogida ha tenido entre los docentes de toda la primaria y se ha difundido de modo sorprendente.
ra los problemas de cambio (a decir verdad, fue el que más nos hizo cavilar). Los resultados del trabajo con el esquema y la respectiva cajita han sido muy satisfactorios, han facilitado a los niños la comprensión y la resolución de los problemas de transformación en sus seis tipos. Lo más interesante es que ellos mismos pueden ejecutar nuevas y diversas formas de resolución para un mismo problema utilizando este material didáctico concreto. Reconocemos que la Cajita para problemas de cambio es la que más acogida ha tenido entre los docentes de toda la primaria y se ha difundido de modo sorprendente.
Nuestra propuesta de trabajo con el material didáctico Cajitas LIRO nos ha traído muchísimas satisfacciones. Facilita el trabajo de los docentes, pero lo más importante es que favorece el aprendizaje de los estudiantes. El uso de las Cajitas LIRO se continúa extendiendo en las aulas del nivel primario de las escuelas públicas y privadas del país y del extranjero, se cuenta con evidencias y testimonios de docentes que nos escriben contándonos cómo les sirven en sus clases y los logros que obtienen sus estudiantes en la ECE. La información sobre las Cajitas LIRO que compartimos en internet tiene ya más de 150000 descargas y hay maestras que han compartido en redes videos de sus estudiantes usando este material. Las cajitas cuentan también con una validación científica a través de investigaciones educativas en el Perú (hay varias investigaciones de tipo experimental donde se han probado, con resultados contundentes), siendo una de ellas la investigación de la misma creadora, para la obtención de su grado de Doctor en Educación.
Las Cajitas LIRO se están tomando como instrumento para investigaciones en didáctica de la matemática infantil en países como Paraguay, Colombia y España. Su aplicación se extiende cada vez más y es gratificante comprobar cómo contribuye a la consolidación de la noción aditiva y a la resolución de los PAEV aditivos, facilitando en los niños la comprensión de los problemas al identificar la estructura de cada tipo de PAEV y ofrecerles la posibilidad de manipular materiales sobre la representación semiótica de cada enunciado. En este sentido, a decir de los mismos usuarios, tiene una ventaja sobre los métodos que trabajan solo sobre representaciones gráficas del problema; las Cajitas LIRO, a diferencia de estos, constituye una propuesta de trabajo con representaciones concretas, que transitan a representaciones gráficas y fácilmente llevan a la representación simbólica; de este modo, responden a las características de los niños para los que han sido creadas, en eso consiste la razón de su efectividad.
Es nuestra intención que esta propuesta de las Cajitas “LIRO”, que a nosotros “nos solucionaron muchos problemas”, sirva a muchos colegas y sobre todo a los niños, para quienes dedicamos todos nuestros esfuerzos.
Autora

Lily Rosas
Doctora en Educación con mención
en Ciencias de la Educación
Doctora en Educación con mención en Ciencias de la Educación por la UNE Enrique Guzmán y Valle – La Cantuta. Magister en Educación con mención en Psicopedagogía por la Universidad San Ignacio de Loyola. Licenciada en Psicología por la Universidad Nacional Mayor de San Marcos. Licenciada en Educación Secundaria por la Universidad Nacional Pedro Ruiz Gallo, especialidad en Ciencias Sociales. Licenciada en Educación Primaria por la Universidad Nacional Federico Villarreal.
Creadora de las Cajitas LIRO, cuenta con especializaciones en Didáctica de la Matemática para la educación primaria, Acompañamiento Pedagógico, Asesoría de Tesis y en Docencia Universitaria, así como diplomados en Tutoría Educativa y Neurociencias aplicadas a la Pedagogía.
Trabajó en el colegio Salesiano Don Bosco del Callao, como Acompañante Pedagógica en PELA Callao, como docente en la Escuela de Post Grado de la UNFV y en la Unidad de Virtualización de la USMP, Especialista de Matemática y Especialista de Formación Docente en el Ministerio de Educación, donde se desempeña actualmente.


Incluye:
- Acceso exclusivo a la plataforma digital y al Grupo interactivo de WhatsApp
- Material digital, batería de problemas y 10 sesiones como modelo
- Certificado por 60 horas por la Universidad Marcelino Champagnat
Fechas:
Del 13 al 17 de febrero de 2023
Horario:
De 8:00 am. a 1:00 pm.
Solo quedan:
- 00Días
- 00Horas
- 00Minutos
- 00
Para comenzar
Compártelo en:
Taller presencial de Estrategias para resolver problemas matemáticos con el Método Liro

Categorías
- Capacitación para el examen de nombramiento (1)
- Curso de biblia (2)
- Ebooks (4)
- Herramientas Digitales (1)
- Inteligencia Artificial (1)
- Lectio divina (6)
- Libros Especiales (1)
- Materiales docentes (1)
- PNL (1)
- Programa Formativo en Diseño de Proyectos de Aprendizaje – Servicio (2)
- Religión (2)
- Ruedas de escucha (1)
- Semana Santa (5)
- Taller Formativo en Diseño de Proyectos (1)
- Taller: La comunidad educativa comprometida (1)
- Taller: La evaluación diagnóstica para el desarrollo de las competencias (2)
- Tutoría (11)
- Webinar (4)
Entradas recientes
- Inteligencia Artificial al Servicio de la Educación Emocional 25 septiembre, 2023
- Conversatorio Virtual: Gestión de la Calidad Educativa para el Éxito 7 junio, 2023
- ¿Vacío existencial en la escuela? 30 enero, 2023
- EDUCACIÓN, LOGOTERAPIA Y ARTE 30 enero, 2023
- Las Cajitas LIRO 26 enero, 2023
